Data Local Iterative Methods For The Efficient Solution of Partial Differential Equations

A cooperation
between

and
.

Funded by
.

Scalar Product: A Performance Study

Introduction:

The scalar product is an important computational kernel in many applications. Here we will use it as a benchmark to evaluate the performance, i.e. the Mflop rate, of several machines. The benchmark program uses an unrolled version of the ddot routine similar to the BLAS package. The code is unrolled by a factor of four to exploit superscalar execution. Note that the program does not compute a general scalar product, but just the (squared) norm of the vector a.

   program scal
   integer n,i,j,loops
   parameter (n=64,loops=2**28/n)
   double precision  a(n), v, s0,s1,s2,s3
   integer ind(n)
   do i=1,n
     a(i)= 1d0
   enddo
C
   do j=1,loops
     s0= 0d0
     s1= 0d0
     s2= 0d0
     s3= 0d0
     do i=1,n,4
       s0= s0+a(i+0)*a(i+0)
       s1= s1+a(i+1)*a(i+1)
       s2= s2+a(i+2)*a(i+2)
       s3= s3+a(i+3)*a(i+3)
     enddo
     v= v+s0+s1+s2+s3
   enddo
   print *, v
   end

The program is run on several different machines shown in the table below, varying n (the vector size) from 64 to 4194304.

Benchmark Results:

All machines show the typical performance degradation of cache-based architectures with increasing vector size. For the Pentium the degradation seems to be least pronounced. However, this is mostly caused by the scaling when compared to processors with superior perfomance. Using the NAG compiler under linux puts the Pentium at a disadvantage, however, it is clear that it would not be competetive with any of the other CPUs even with a better optimizing compiler. A quite similar picture is obtained with the Portland Group F77 compiler (PG F77). Out of cache, that is with vector sizes of more than 2¹⁸=262144 the Pentium Pro actually beats the SGI Indigo which (as the oldest of the architectures) has the lowest main memory bandwidth. Only the Power PC 604 based machines show similarly poor performance.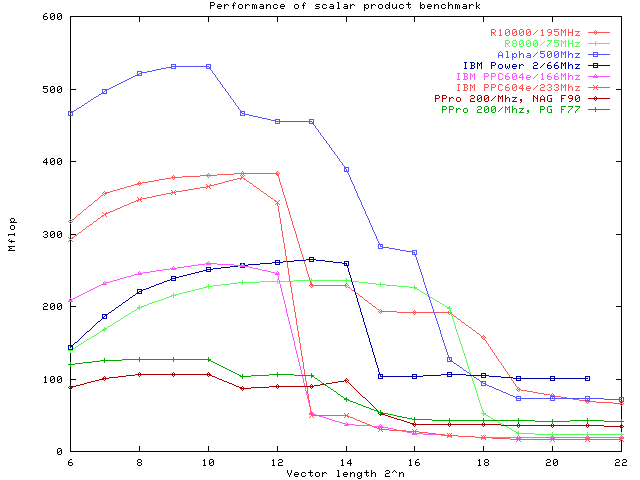

The newer SGI design based on the R10000 chip in the Origin 2000 architecture clearly has better out-of-cache performance, but for vector sizes between 2¹³and 2¹⁷ (that is data fitting in the secondary off chip cache) both R8000 Indigo and R10000 Origin have nearly the same performance. The best out-of-cache performance is still seen for the IBM Power 2 machine, though its 66 MHz CPU does haeve a comparatively low peak. For the age of its basic design it still has remarkable performance, due to its high bandwidth memory system. In this comparison, however, the fastest CPU is clearly found in the Alpha workstation. Except in a small window, where its 2MB cache is too small (while the 4MB of the SGI Origin can still hold the data), it clearly outperforms the competition. The staircase in the Mflop plot indicates it three-layered cache architecture with 8KB, 96 KB and 2MB size, respectively. In out-of-cache performance it does not quite reach the IBM Power 2 architecture, but surprisingly, it is quite competetive with all others, including the SGI Origin 2

Note that though already quite impressive, these are not yet optimal results. Steven Fried from Microway, for example, reports up to 950 Mflop for the Alpha in his optimization tutorial.

Computing a True Scalar Product:

In a few more experiments we will now focus on the Alpha and the R10000 machine. The obvious modification to the above code is to use two different vectors a and b and thus compute a true scalar product. The analogous performance plot is given below: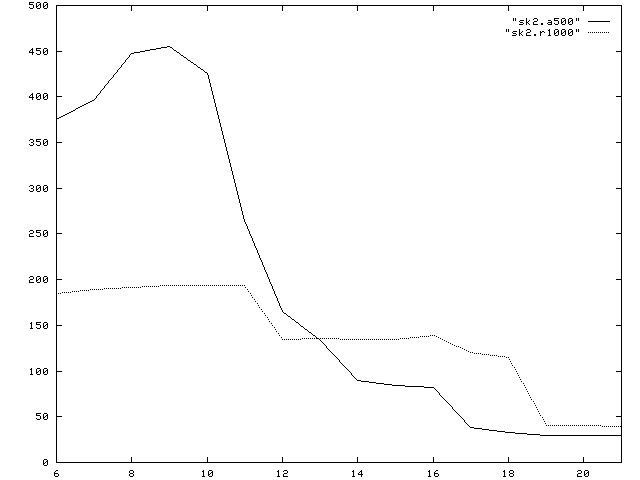

Here the comparison has somewhat shifted. While the Alpha remains dominant for small vector lengths, and is competetive in its out-of-cache performance, there is an intermediate region, where the R10000 is significantly faster, not only due to its larger off-chip cache, but also because it obviously produces better hit ratios.

Effect of Indirect Addressing:

Finally, we look into the effect of indirect addressing. This is important, since all data structures for unstructured meshes and general sparse matrices must employ some kind of indirect addressing. Such data structures can e.g. be implemented as linked lists using languages like C or C++. In FORTRAN this must be simulated using index arrays. The following program is an extreme case, where to access each element in either the vector a or b, an index must be loaded form an index array. Note that we have set up the benchmark such, that like in a linked list each index can only be computed, when its predecessor has been brought to the CPU. This computation is therefore latency limited rather than bandwidth limited as the previous examples. The progam is

      program scal
      integer n,i,j,ii,jj,loops
      parameter (n=64,loops=2**26/n)
      double precision  a(n), b(n), v, s0,s1,s2,s3
      integer ind(n), null
      read *, null
      do i=1,n
         a(i)= 1d0+null
         b(i)= 1d0+null*null
         ind(i)= i+1+null
         null= 2*null
      enddo
      ind(n)= 1
C
 10   do j=1,loops
      s0= 0d0
      s1= 0d0
      s2= 0d0
      s3= 0d0
      ii= 1
      jj= ind(ii)
      do i=1,n,4
         s0= s0+a(ii)*b(jj)
         ii= ind(jj)
         jj= ind(ii)
         if(ii .gt.n) goto 19
         s1= s1+a(ii)*b(jj)
         ii= ind(jj)
         jj= ind(ii)
         if(ii .gt.n) goto 19
         s2= s2+a(ii)*b(jj)
         ii= ind(jj)
         jj= ind(ii)
         if(ii .gt.n) goto 19
         s3= s3+a(ii)*b(jj)
         ii= ind(jj)
         jj= ind(ii)
         if(ii .gt.n) goto 19
      enddo
 19   continue
      v= v+s0+s1+s2+s3
      enddo
      print *, v
      end

Note that a dummy variable null is used to prohibit the compiler to use any compile time information to improve the program performance. Also note that despite the indirect access, the data is still stored with a stride 2 layout. Besides resulting in a stride of 2, there is no reallly irregular access pattern involved. Thus the performance degradation is a pure latency problem.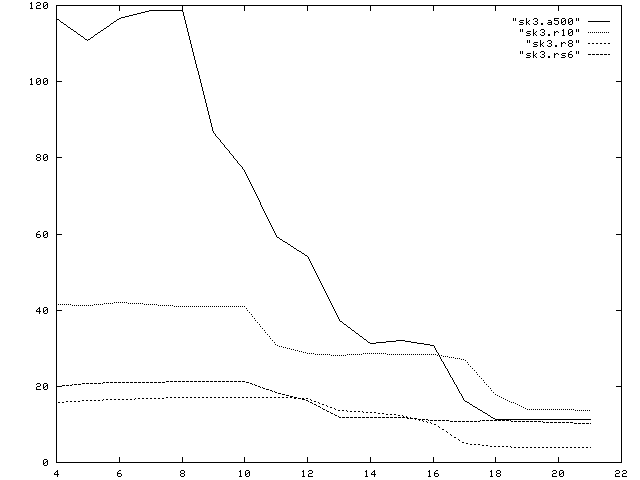

Clearly, none of the machines is even coming close to its peak performance. The Alpha performance may still be considered reasonable, when the data is small enough to fit in the on chip cache. For off-chip cache performance, the Alpha and the R10000 both reach approximately 30-40Mflops. For the Alpha this is a mere 4% of its peak performance. The main memory performance is 11 and 13 Mflop for the Alpha and the R10000, respectively which corresponds to 1.1% of the peak performance for the Alpha chip. In case of the R8000 only 4 Mflop of out-of-cache performance are obtained. Again, recall that this is for a CPU capable of 300 Mflops peak performance.