rb4.F Program
Description
File Name:rb4.F
Description:
The algorithms rb2.F and
rb3.F both try to reuse the
data of the red update sweep in the black sweep soon
enough so that the data is still in the cache. They
do this by melting the operations for the red and
black update sweeps together. However, if several
successive red-black Gauss-Seidel relaxations are
performed the data in the cache is not reused between
different relaxation sweeps if the grid is to big to
fit in the cache. The present algorithm addresses
this issue.
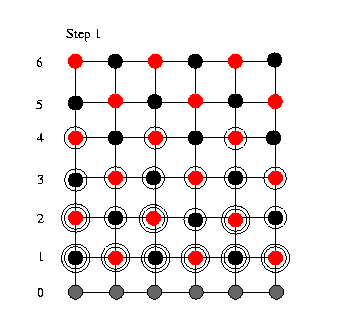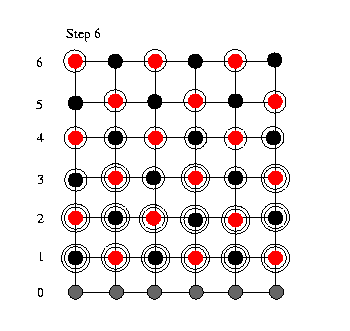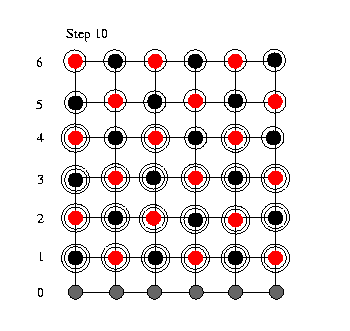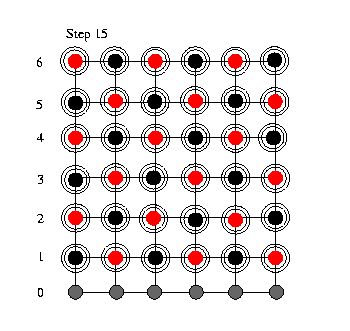
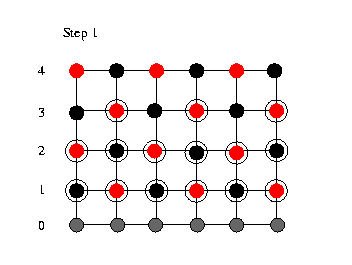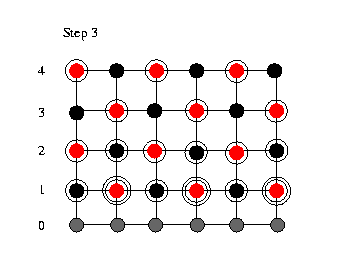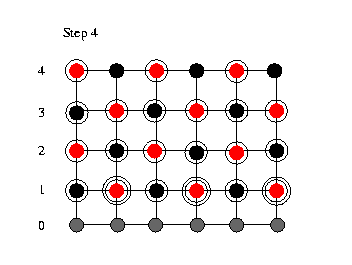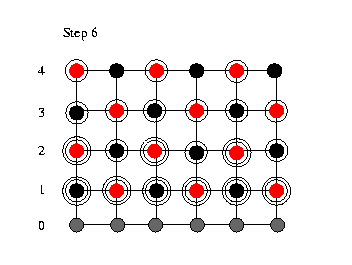 Assume that we
melt two red-black Gauss-Seidel sweeps together. We
start in a situation where we have updated the first
rows in pairs (see figure above; circles indicate
number of performed relaxations). In this situation
we are able to update the red points in row 1 the
second time. We now continue to update the red nodes
in row 4. Once all of the red nodes in row 4 have
been updated all of the black nodes in row 3 can be
updated. Then all red nodes in row 2 are updated the
second time and as a consequence also the black nodes
in row 1 are updated the second time. Assume that we
melt two red-black Gauss-Seidel sweeps together. We
start in a situation where we have updated the first
rows in pairs (see figure above; circles indicate
number of performed relaxations). In this situation
we are able to update the red points in row 1 the
second time. We now continue to update the red nodes
in row 4. Once all of the red nodes in row 4 have
been updated all of the black nodes in row 3 can be
updated. Then all red nodes in row 2 are updated the
second time and as a consequence also the black nodes
in row 1 are updated the second time.
 We now are in
a wavefront like situation where we have updated some
of the lines once and some twice. Then we update the
(red) nodes in line 5 and cascade down three rows
updating alternately black and red nodes. In this
way, we move the wavefront throught the grid until we
reach the last row of the grid (step 9). The height
of the wavefront is the number of simultaneously
performed update sweeps. The width of the wavefornt
is twice the number of update sweeps. In the shown
case of two simultaniously performed update sweeps
this means that the wavefront is 4 rows wide. At the
top of the grid (step 10 to 15) the wavefront shrinks
down to one single row. So that at the end of the
relaxation sweep only the black nodes in the last row
remains for update. We now are in
a wavefront like situation where we have updated some
of the lines once and some twice. Then we update the
(red) nodes in line 5 and cascade down three rows
updating alternately black and red nodes. In this
way, we move the wavefront throught the grid until we
reach the last row of the grid (step 9). The height
of the wavefront is the number of simultaneously
performed update sweeps. The width of the wavefornt
is twice the number of update sweeps. In the shown
case of two simultaniously performed update sweeps
this means that the wavefront is 4 rows wide. At the
top of the grid (step 10 to 15) the wavefront shrinks
down to one single row. So that at the end of the
relaxation sweep only the black nodes in the last row
remains for update.
The technique can be generalized so that the nodes
can be updated m times in one sweep throught
the grid obtaining the same results we would get if
m sweps of the standard red-black
Gauss-Seidel algorithm were applied.
Comment:
Instead of doing m successive sweeps
through the grid updating each node once we do just
one sweep throught the grid updating each node
m times. Hence, the grid is transfered from
main memory to the cache once instead of m
times. However, this is only correct if
m*2+2 rows of the grid fit in the cache.
Results:
Memory access behaviour
| Size |
MBytes
/sec |
% of all access which go
into |
| ± |
1. Level |
2. Level |
3. Level |
Memory |
|
2 sweeps performed together |
| 16 |
1769.8 |
4.8 |
95.1 |
0.0 |
0.0 |
0.0 |
| 32 |
2254.1 |
4.3 |
80.9 |
14.8 |
0.0 |
0.0 |
| 64 |
3030.3 |
0.1 |
90.4 |
9.3 |
0.2 |
0.0 |
| 128 |
2012.5 |
0.0 |
72.2 |
24.3 |
3.5 |
0.0 |
| 256 |
1535.1 |
6.9 |
33.8 |
56.1 |
3.2 |
0.0 |
| 512 |
844.0 |
6.8 |
31.5 |
57.4 |
2.5 |
1.8 |
| 1024 |
747.5 |
6.7 |
26.6 |
59.1 |
5.8 |
1.8 |
| 2048 |
570.9 |
6.5 |
33.8 |
42.7 |
15.2 |
1.8 |
|
3 sweeps performed together |
| 16 |
1813.4 |
5.2 |
94.7 |
0.0 |
0.0 |
0.0 |
| 32 |
2144.4 |
4.3 |
74.7 |
21.0 |
0.0 |
0.0 |
| 64 |
2894.3 |
0.1 |
83.9 |
15.8 |
0.1 |
0.0 |
| 128 |
2081.1 |
0.1 |
63.0 |
34.7 |
2.2 |
0.0 |
| 256 |
1622.0 |
7.0 |
29.3 |
61.6 |
2.1 |
0.0 |
| 512 |
1026.5 |
7.1 |
32.1 |
57.3 |
2.3 |
1.2 |
| 1024 |
815.8 |
6.8 |
30.2 |
53.2 |
8.6 |
1.2 |
| 2048 |
627.3 |
6.6 |
35.5 |
40.7 |
15.9 |
1.2 |
Runtime behaviour
| Size |
MFlops
/sec |
% of cycles used for |
| ± |
Base |
Exec |
Cache |
DTB |
Branch |
R dep |
Nops |
| 2 sweeps performed
together |
| 16 |
332.1 |
4.4 |
119.8 |
68.4 |
0.2 |
3.5 |
10.2 |
27.3 |
5.8 |
| 32 |
420.6 |
3.0 |
124.7 |
81.9 |
4.9 |
5.0 |
7.2 |
14.7 |
8.0 |
| 64 |
541.9 |
0.5 |
142.2 |
107.9 |
1.7 |
10.7 |
4.4 |
9.4 |
7.6 |
| 128 |
359.5 |
-0.9 |
121.0 |
85.2 |
5.5 |
26.6 |
0.0 |
0.0 |
4.6 |
| 256 |
294.3 |
-0.1 |
111.8 |
55.0 |
41.6 |
9.1 |
0.1 |
0.0 |
6.1 |
| 512 |
161.7 |
-0.2 |
104.7 |
30.8 |
66.0 |
5.0 |
0.1 |
0.0 |
3.0 |
| 1024 |
143.0 |
-0.1 |
103.4 |
26.6 |
70.5 |
3.8 |
0.0 |
0.0 |
2.6 |
| 2048 |
109.1 |
0.1 |
103.5 |
20.8 |
76.3 |
4.0 |
0.0 |
0.0 |
2.3 |
| 3 sweeps performed
together |
| 16 |
341.8 |
4.1 |
117.7 |
65.0 |
0.3 |
3.6 |
8.5 |
31.0 |
5.2 |
| 32 |
400.3 |
2.9 |
120.8 |
76.8 |
7.4 |
5.8 |
6.5 |
13.9 |
7.5 |
| 64 |
517.5 |
0.7 |
137.0 |
100.3 |
2.8 |
13.4 |
4.0 |
8.7 |
7.1 |
| 128 |
372.0 |
1.1 |
124.5 |
79.3 |
16.2 |
19.5 |
0.3 |
3.7 |
4.4 |
| 256 |
311.4 |
0.1 |
111.6 |
58.0 |
38.6 |
8.4 |
0.1 |
0.0 |
6.4 |
| 512 |
197.3 |
0.0 |
106.2 |
37.5 |
59.3 |
5.8 |
0.0 |
0.0 |
3.6 |
| 1024 |
156.3 |
-0.2 |
104.3 |
29.1 |
67.8 |
4.8 |
0.0 |
0.0 |
2.8 |
| 2048 |
119.9 |
0.0 |
104.1 |
23.5 |
73.2 |
4.8 |
0.0 |
0.0 |
2.6 |
Table
explanation
|





 Assume that we
melt two red-black Gauss-Seidel sweeps together. We
start in a situation where we have updated the first
rows in pairs (see figure above; circles indicate
number of performed relaxations). In this situation
we are able to update the red points in row 1 the
second time. We now continue to update the red nodes
in row 4. Once all of the red nodes in row 4 have
been updated all of the black nodes in row 3 can be
updated. Then all red nodes in row 2 are updated the
second time and as a consequence also the black nodes
in row 1 are updated the second time.
Assume that we
melt two red-black Gauss-Seidel sweeps together. We
start in a situation where we have updated the first
rows in pairs (see figure above; circles indicate
number of performed relaxations). In this situation
we are able to update the red points in row 1 the
second time. We now continue to update the red nodes
in row 4. Once all of the red nodes in row 4 have
been updated all of the black nodes in row 3 can be
updated. Then all red nodes in row 2 are updated the
second time and as a consequence also the black nodes
in row 1 are updated the second time. We now are in
a wavefront like situation where we have updated some
of the lines once and some twice. Then we update the
(red) nodes in line 5 and cascade down three rows
updating alternately black and red nodes. In this
way, we move the wavefront throught the grid until we
reach the last row of the grid (step 9). The height
of the wavefront is the number of simultaneously
performed update sweeps. The width of the wavefornt
is twice the number of update sweeps. In the shown
case of two simultaniously performed update sweeps
this means that the wavefront is 4 rows wide. At the
top of the grid (step 10 to 15) the wavefront shrinks
down to one single row. So that at the end of the
relaxation sweep only the black nodes in the last row
remains for update.
We now are in
a wavefront like situation where we have updated some
of the lines once and some twice. Then we update the
(red) nodes in line 5 and cascade down three rows
updating alternately black and red nodes. In this
way, we move the wavefront throught the grid until we
reach the last row of the grid (step 9). The height
of the wavefront is the number of simultaneously
performed update sweeps. The width of the wavefornt
is twice the number of update sweeps. In the shown
case of two simultaniously performed update sweeps
this means that the wavefront is 4 rows wide. At the
top of the grid (step 10 to 15) the wavefront shrinks
down to one single row. So that at the end of the
relaxation sweep only the black nodes in the last row
remains for update.
