Data Local Iterative Methods For The Efficient Solution of Partial Differential Equations

A cooperation
between

and
.

Funded by
.

Data Locality Optimizations for Multigrid Methods

Overview:

Multigrid is one of the most attractive algorithms for the solution of large sparse systems of equations that arise in the solution of PDEs. The efficiency of multigrid algorithms has been shown theoretically and in numerous practical applications. In terms of the number of arithmetic operations, multigrid methods are asymptotically optimal, that is the number of operations is only proportional to the number of unknowns.

Our studies, however, showed that straightforward implemented multigrid methods are not able to exploit the full performance of current microprocessors. The reason for this is, that the CPU is stalled most of the time by data cache misses. The main goal of our research therfore is to improve the data locality of multigrid methods to achieve a reasonable fraction of the peak performance of current RISC CPUs.

The smoother - in our case red-black Gauss-Seidel - is one of the most computationally expensive parts of a multigrid algorithm. Therfore, improving the performance of this relatively small module can cause a significant improvement of the performance of the whole multigrid method. In the figure below you can see the distribution of CPU cycles on a DEC PWS 500au upon the components of a 2D standard multigrid method (linear interploation, half injection and red-black Gauss-Seidel) with 4 presmoothers and no postsmoothers using a 5-point discretisation for different grid sizes. If less presmoothers are applied the per cent of cycles spend in the relaxation method drops. However, even with only two presmoother the relaxtion still consumes 71% of all CPU cyles on a 1024x1024 grid.

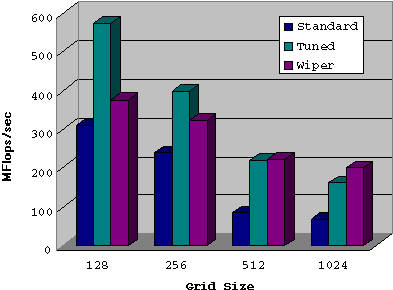
The Performance of the Smoother:

As a consequence we started our data locality studies with the red-Black bauss-Seidel smoother. A small overview of the achieved performance of a standard red-black Gauss-Seidel compared to a for data locality tuned version is shown in the figure below.

The figure clearly shows that the performance can be improved for every grid size; even for the small ones. However, the greatest improvements can be achieved when the grid does not fit completely in one of the caches of the memory hierachy and the data must be fetched from main memory. In this case the improvement in the MFlops/sec rates can be more than a factor of 4.

The Performance of the Multigrid Method:

We plugded two optimized versions (tuned and wiper) of red-black Gauss-Seidel into our multigrid program and measured a reasonable speedup for all grid sizes. However, the greatest improvements of more than a factor of 3 showed up for the larger grid sizes. Taking Amdahl's law into account this is a nearly optimal result.

To achive an additional speedup it is necessary to fuse the relaxation with the restriction and interpolation operation. A description of the technical details of these techniques and some results on a SGI Power Indigo with R8000 processor can be found in:

• Linda Stals, Ulrich Rüde.
  Techniques for improving the data locality of iterative methods.
  Technical Report MRR97-038, School of Mathematical Sciences, Australian National University.
  PS (238K)