 |
Data Local Iterative Methods For The Efficient Solution of Partial Differential Equations |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
|
A cooperation Funded by |
Data Locality Optimization OverviewR/B Fusing:
Consequently, we update the red nodes in a row i and the black nodes in row i-1 in pairs. However, some special treatment must be used for the update of the red nodes in row 1 and the update of the black nodes in row n-1. Instead of doing a red sweep and then a black sweep, we just do one sweep of the grid updating the red and black nodes as we move through. The consequence is that the grid must be transfered from main memory to cache only once per update sweep instead of twice. This is true as long as the lines needed for the pairwise update fit in the cache. There are two ways to implement this idea. The first possibility is to update each black node as soon as possible. This means that a red node in row i and the black node in row i-1 directly underneath it are updated in pairs. The second possibility is to update a certain amount of red nodes which fit in the cache and then update all of the black nodes which can be updated as a consequence of this. A typical amount of nodes would be the number nodes in one line of the grid. Sweep Blocking:The technique above applies to one single red-black relaxation sweep. However, if several successive red-black Gauss-Seidel relaxations are performed the data in the cache is still not reused between different relaxtion sweeps if the grid is to big to fit in the cache. A common data locality optimization technique is loop blocking or loop tiling. The loop is transformed in a way so that the accesses are performed successive on parts (blocks or tiles) of the array rather than the whole array at once. The size of the blocks is choosen appropriate to the size of the cache and the data within a block is reused as many times as possible before the computation switches to the next block of the array.
If a red node in line i is updated the first time the black node in line i-1 directly underneath can also updated the first time. As a consequence the red node in line i-2 and the black node in line i-3 directly underneath can be updated the second time and so on till the red node in line i-m*2+2 and the black node in line i-m*2+1 are updated the mth time. This can be done for all red nodes in line i. In the next step the whole block is moved up to line i+1. Of course, the lower and upper bound of the grid must be handled slightly different. Like the technique described above, there are several ways to implement the sweep blocking technique. One possibility is to update the nodes underneath a red node as soon as possible. The other possibility is to update several red nodes which fit in the cache (e.g. on line of the grid) and then update all the nodes which can be updated as a consequence of this. And there are several combinations of both techniques possible. Array Padding:Since a cache is much smaller than main memory a certain placement strategie is needed. A typical placement strategie is to use a function like addr mod cache size to calculated the place where the data is located in the cache. Caches which use such a placement strategie are called direct mapped. Other possible placement strategies are implemented in set associativ or fully asssociativ caches where the data can be placed in a set of places respectively in all places of the cache.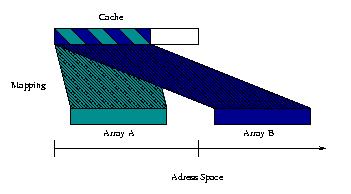 
If we assume direct mapped or set associativ caches two different memory locations can compete for the same cache line and cause conflict misses althougt the data would fit in the cache. There are two possible situations: self interference and cross interference. If two memory locations of the same array compete for the same cache line we have self interference. If the memory location are within two different arrays this is called cross interference. Both effects can be reduced by adding a small padding (extra array elements) between arrays or parts of the array such that the competing memory locations are mapped to different locations in the cache. However, it is very difficult to choose the optimal amount of padding. Prefetching:Prefetching is a technique which tries to load the data into one of the upper levels of the memory hierarchy before the data is actually needed. Prefetching requires a special CPU instruction which can be used by the compiler or assembler programmer to issue the loading from main memory. If the data was loaded succesfully from main memory to the cache an access can be performed with a much smaller latency. More Techniques:
|
When implementing the standard
red-black Gauss-Seidel algorithm, the usual practice
is to do one complete sweep of the grid from bottom
to top updating all the red nodes and then one
complete sweep updating all of the black nodes. If a
5-point stencil is placed over one of the black nodes
(see figure) then we can see that all of the red
points it touches are up to date as long as the red
node above it is up to date.
The loop blocking
technique is not directly applicable because of the
data dependencies of the standard red-black
Gauss-Seidel. A second update sweep can be applied as
soon as all neighbors are updated the first time.
Hence, if a certain block is updated several times
the block would shrink by two lines (one line with
red points and one with black points) each iteration.
To keep a constant sized block the block must slide
through the grid.
